Theory and Usage of Linear Regression

linear regression is an approach for modeling the relationship between a scalar dependent variable y and one or more explanatory variables (or independent variables) denoted X. We will need a function that maps from our feature space to label values. We can choose a linear function, quadratic, logarithmic, etc, so long as the type of function we choose to appropriate the data we’re working with.

As a supervised learning method, linear regression can be used to solve two kinds of problem: regression problem and classification problem. When the target variable that we’re trying to predict is ordinal, such as price and temperature, we call the learning problem a regression problem. When the value we are predicting takes on a finite number of discrete values each arbitrarily identifying an abstract class, we call that a classification problem.

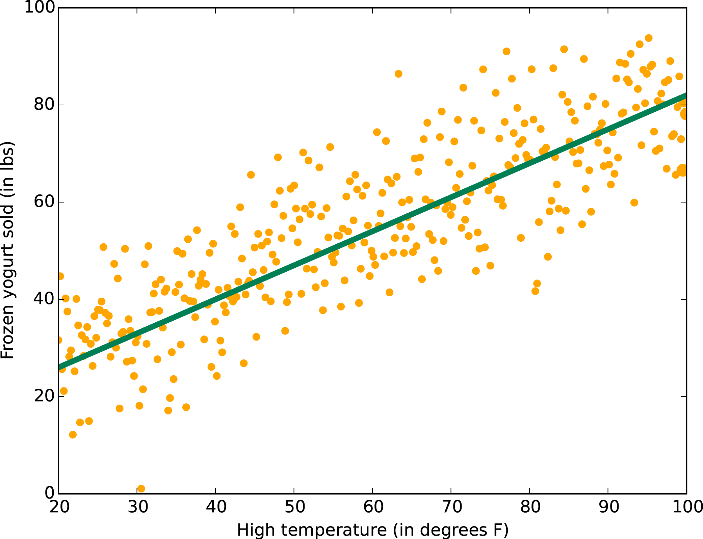
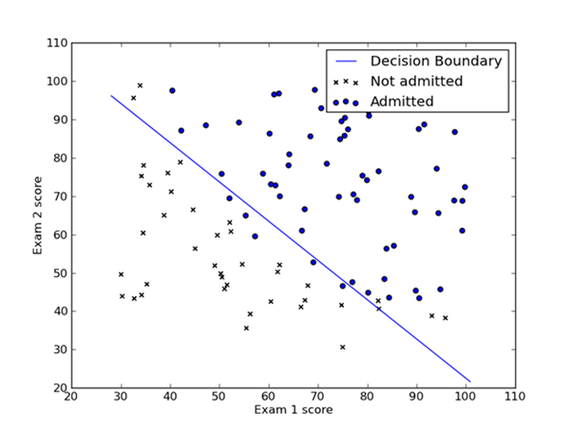
For linear functions of more than one variable, there are more than one slope term, where each term corresponds to the relative slope over each variable. Linear regression involves searching through the set of possible slope and intercept values, and finding that set whose corresponding linear surface best fits our training data. This choosing of an ideal function from a class is often called fitting or training the linear model.

To do this, we need to define some cost function, which will compute how well any specific function performs. Training for linear regression, like for any parametric method, is a matter of choosing a set of parameters that minimize this cost function. As stated above, the algorithm will find a set of slope and intercept values that best fit our training data. The way this is computed is via an cost function calculated between the linear surface value, and true label value. This error function is large when the linear surface poorly fits the training labels. The exact nature of this process will be described shortly. Let’s first consider when and how linear functions can be used to predict values.