Model Choice

In the case of linear regression, we choose as our model the class of linear functions. A linear function f(x) over m variables has a general form $$\hat{y} = h(\vec{x},\vec{w})=w_0+w_1x_1 +w_2x_2 +\dots+w_mx_m$$ where $x$ is a vector in feature space, $x_1, x_2,\dots, x_m$ are the elements of that vector, $w$ is a vector of weights. Any function of this form, when plotted over the variables from $x_1$ to $x_m$, will describe a plane or hyperplane.

Our goal is to find a linear function that predicts the labels based on the feature values for any point. We find a linear function that predicts the labels within our training data with high accuracy. ‘Finding’ a linear function here refers specifically to finding a set of weights that maximize accuracy or, equivalently, minimize loss, on our training set.

With no risk of confusion, we will drop the $w$ in $h(w, x)$, and write it simply as $h(x)$. If we concatenate a 1 to the beginning of any datapoint vector $x$, then our linear function can be expressed as a dot product: $$\hat{y} = h(\vec{x})=\sum_{i=0}^{m}w_ix_i=\vec{w}\cdot \vec{x}$$

To take the constant terms into account, we shall restructure our feature matrix as

$$\textbf{X}= \begin{bmatrix} 1 & x_{11} & \dots & x_{1m}\\ 1 & x_{21} & \dots & x_{2m}\\ \vdots & \vdots & \ddots & \vdots\\ 1 & x_{n1} & \dots & x_{nm}\end{bmatrix}$$

And We denote those biases, constant terms, as w0, and define our weight vector correspondingly as:

$$\vec{w}=\begin{bmatrix} w_0 \\ w_1 \\ \vdots \\ w_m \end{bmatrix}$$

Given a set of weights, we can compute the linear prediction function for every point in our training set at once, with a simple matrix multiplication.

$$\vec{\hat{y}} = \begin{bmatrix} 1 & x_{11} & \dots & x_{1m}\\ 1 & x_{21} & \dots & x_{2m}\\ \vdots & \vdots & \ddots & \vdots\\ 1 & x_{n1} & \dots & x_{nm}\end{bmatrix}\begin{bmatrix} w_0 \\ w_1 \\ \vdots \\ w_m \end{bmatrix} = \begin{bmatrix} w_0 + w_1x_{11} + \dots + w_mx_{1m}\\ w_0 + w_1x_{21} + \dots + w_mx_{2m} \\ \vdots \\ w_0 + w_1x_{n1} + \dots + w_mx_{nm} \end{bmatrix}$$

Notice the right side of the equation is a set of linear functions, given a common set of parameters applied to every point in our dataset. If all our datapoints happens to fall on a single plane, then there exists some weights with which our model will perfectly fit the data. This means that $\hat{y}$, will be equal to the true label vector y. In practice, this is never the case, the data does not fall perfectly on a linear surface, then there is no perfectly fitting set of weights.

Our training algorithm should find the “best” set of weights. We define the best set as those that minimize a cost function, given by

$$J(\vec{w})=\sum_{i=1}^n (h({x_i})-y_i)^2$$

where n is the number of datapoints in our training dataset. The element $x_i$ refers to the $i_{th}$ row of our training data matrix, $X$, and the term $y_i$ refers to the corresponding label for that point, which is the $i^{th}$ element in the label vector $y$.

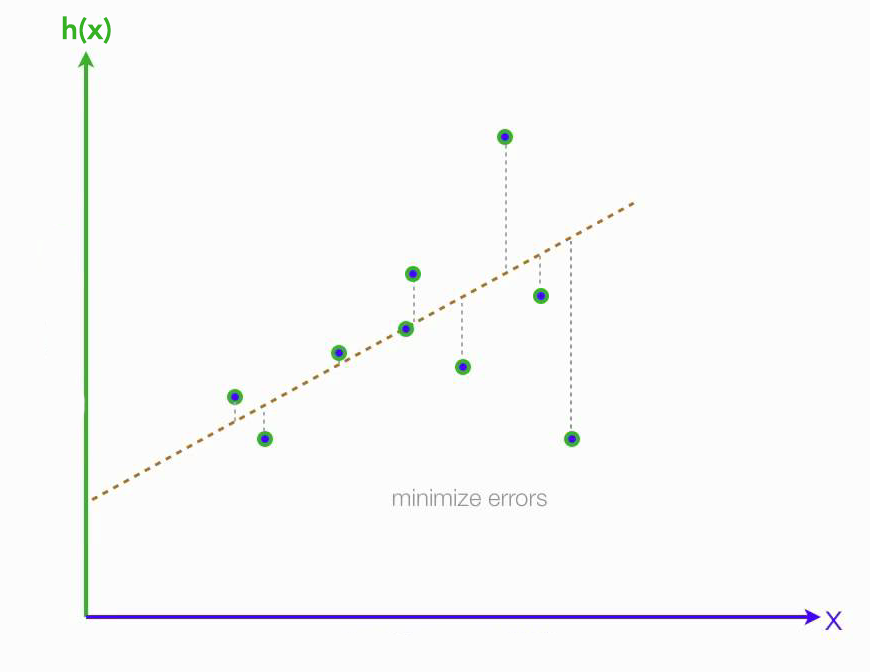
sum-squared error function

This function takes the summed distances between all the predictions for every point and their corresponding labels. In general, it shrinks as the predicted values get closer to the true labels. This is called the sum-squared error function.