Polynomial Case Example

Let’s attempt to fit a polynomial model to the data set where there is only one feature. Imagine we want to fit a quadratic polynomial to our dataset. Then our the data set has a matrix representation

$$\textbf{X}=\begin{bmatrix}1 & x_1 & x_1^2\\ 1 & x_2 & x_2^2\\ \vdots & \vdots & \vdots \\ 1 & x_n & x_n^2 \end{bmatrix}\vec{y}=\begin{bmatrix}y_1 \\ y_2 \\ \vdots \\ y_n\end{bmatrix}\vec{w}=\begin{bmatrix}w_0 \\ w_1 \\ w_2\end{bmatrix}$$

Notice that coefficients corresponding to features have been dropped because number of features $m=1$. This yields the model which is graphically represented like this.

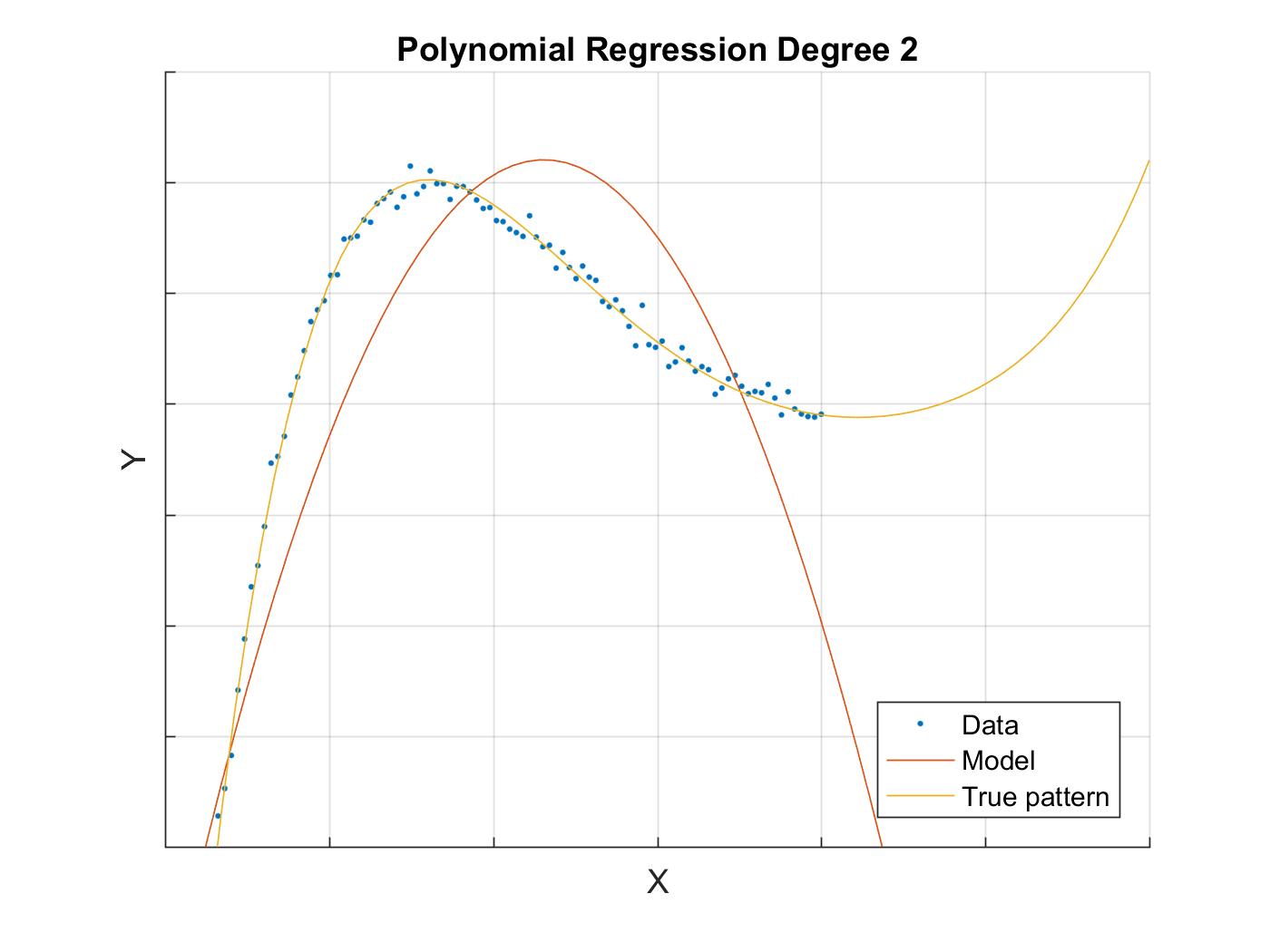
We can see that the model is not that accurate in the range of data and if we go beyond the range of data the global behaviour of our model kicks in. We see that the model is insufficient in the regions away from the training data as well as the data range itself. In particular, it overshoots vastly for more positive datapoint.

Let’s attempt to fit a polynomial of degree $10$ to our data to see if it makes a better prediction. Because we have only one feature, the number of weights that we can expect to solve for is $10 + 1$, which is $11$. The data set is represented in the matrix notation as

$$\textbf{X} = \begin{bmatrix}1 & x_1 & \dots & x_1^{10}\\ 1 & x_2 & \dots & x_2^{10}\\ \vdots & \vdots & \ddots & \vdots\\ 1 & x_n & \dots & x_n^{10} \end{bmatrix}\vec{y} =\begin{bmatrix}y_1\\ y_2 \\ \vdots \\ y_n \end{bmatrix} \vec{w}= \begin{bmatrix} w_0\\ w_1\\ \vdots \\ w_{10}\end{bmatrix}$$

The line of best fit is presented below

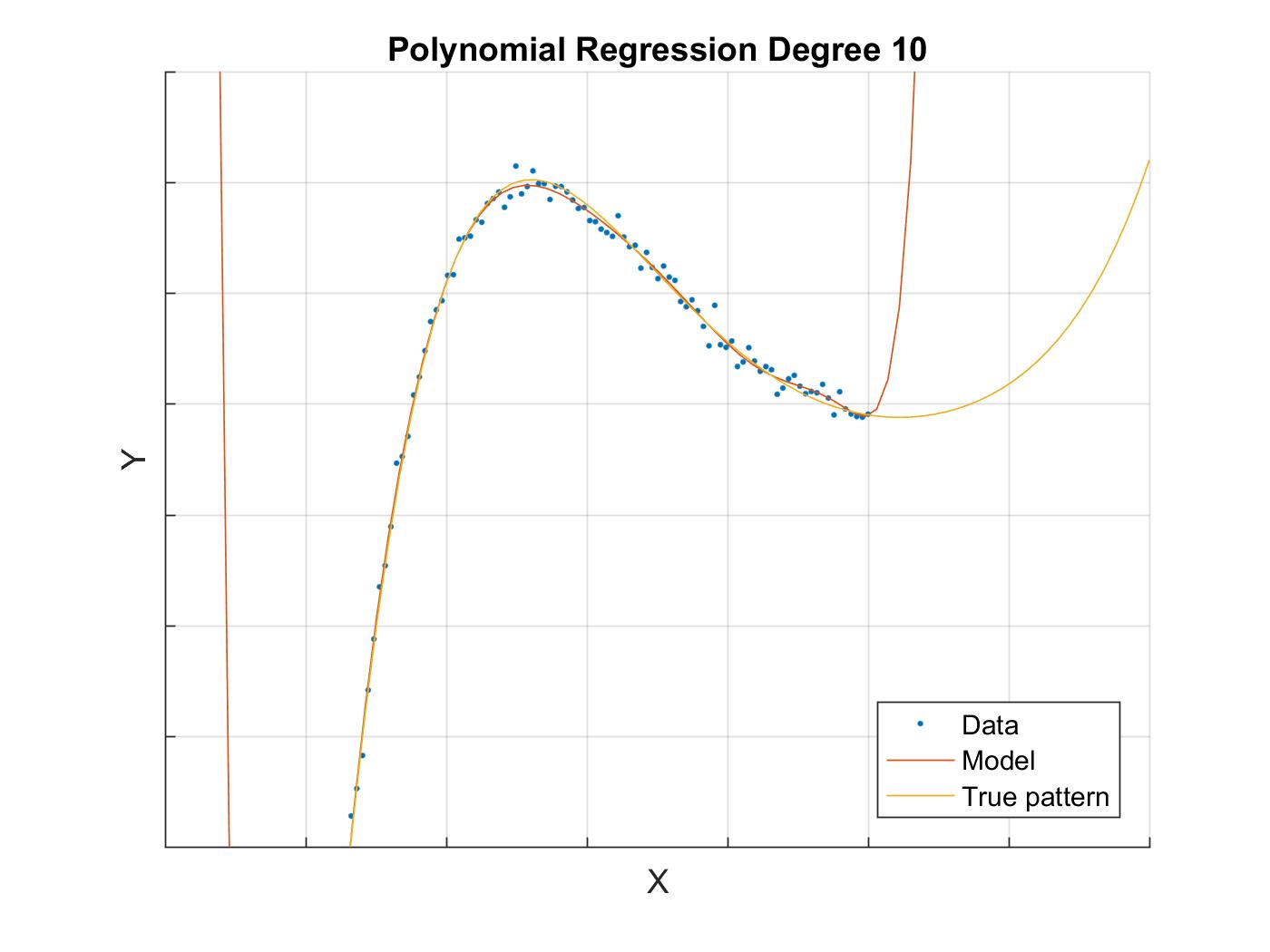
The fitting is more successful than the one previously defined in the range of the training data because our prediction follows the data very closely. The noise that our data has is present in our model. We can see that our model oscillates from one data point to another. This is an example of overfitting. However, global behaviour of the model provides even worse prediction outside of the training data range, because it explodes in magnitude. This proves that one needs to be careful with using regression models outside of the range of the training data that was used to train the model. Additionally, the degree 10 example demonstrates how overfitting can occur if the model is chosen incorrectly.

Finally, let’s attempt using a fifth-degree polynomial to see how successful it will be. Because we have only one feature we have $1+5*1=6$ weights. The data set and the weights are represented in matrix notation as

$$textbf{X} = \begin{bmatrix}1 & x_1 & \dots & x_1^{5}\\ 1 & x_2 & \dots & x_2^{5}\\ \vdots & \vdots & \ddots & \vdots\\ 1 & x_n & \dots & x_n^{5} \end{bmatrix}\vec{y} =\begin{bmatrix}y_1\\ y_2 \\ \vdots \\ y_n \end{bmatrix} \vec{w}= \begin{bmatrix} w_0\\ w_1\\ \vdots \\ w_{5}\end{bmatrix}$$

This yields the regression curve shown below.

This model is very successful in fitting our data and the true pattern. However, notice that in the region outside of the data range still deviates from the true pattern. Generally, the regression model should only be used in the range of training data, because outside of the range proper fitting is not guaranteed. If the degree of the polynomial approximation is lower than the degree of the true pattern, the model will perform poorly inside and outside the range of training data. If the degree of the polynomial approximation is higher that the degree of the true pattern, the model will overfit inside the range of training data and it will behave very unexpectedly outside of the training range. Even if the degree of the model matches the degree of the true pattern we cannot guarantee precise fitting outside of the training range because the impurities introduced into our model by the noise in data will extrapolate as we move away from the training range.