Advantages and Disadvantages

Obviously, the linear regression model is only meant to fit data where we believe there is a linear trend between our features and the value we mean to predict. As a result, the linear regression model is not useful for modeling trends or data that we know to be more complex.

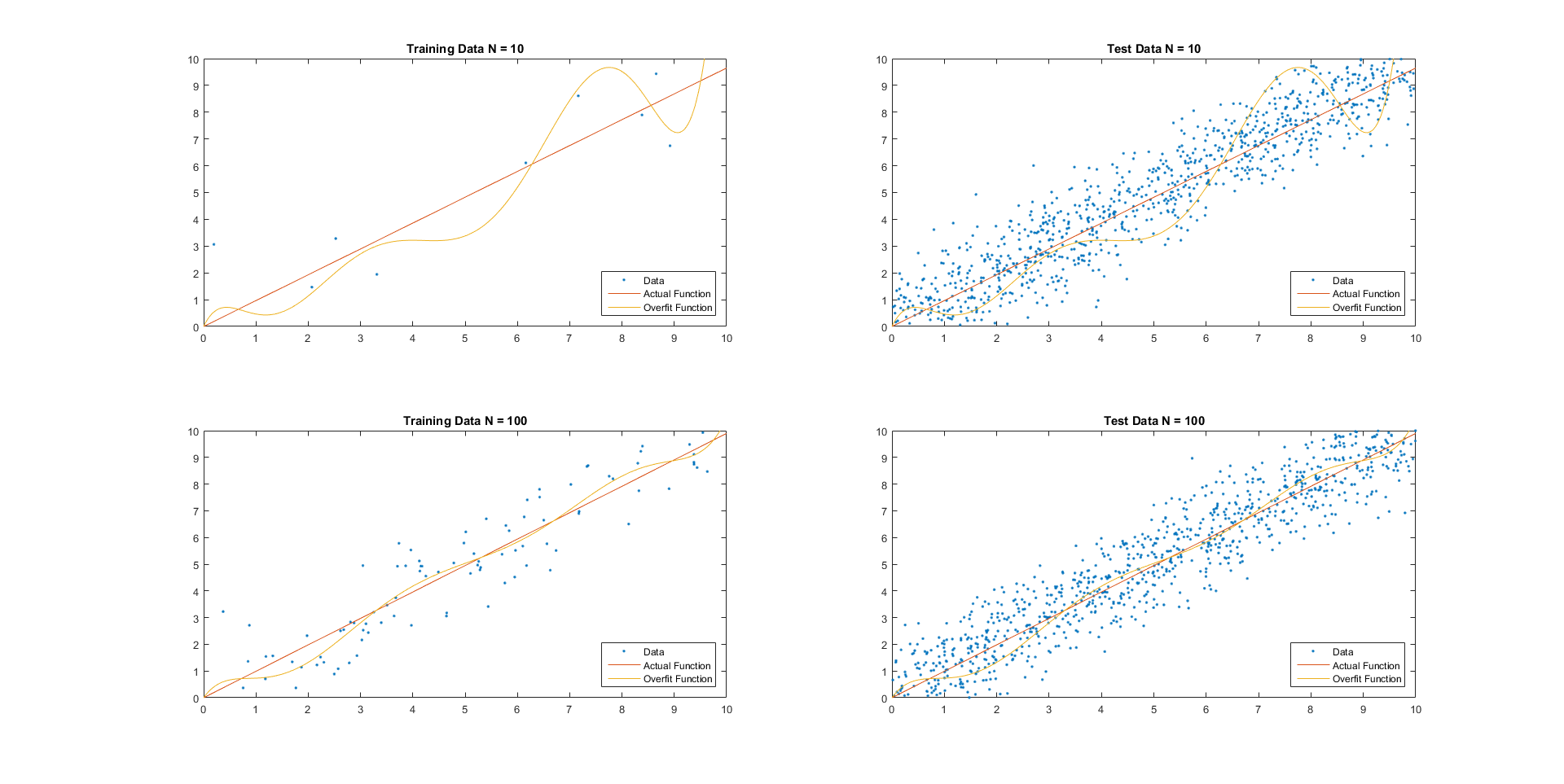
Higher order regression models are available, as very simple extensions to linear regression. Note that any regression model assumes that a certain model type is correct for the data. There is no simple method for deciding the correct model type, or which regression model would fit best. Determining this is typically an empirical task, involving testing and evaluating.

Direct model regression, of which linear regression is the simplest example, can be used together to find ideal trends. This sort of method involves fitting several different degree models to a dataset, and then comparing their results on a validation set, with the best fit informing us as to the actual shape of the model.

Alternatively, one could train a model on random subsets of the training data, checking to see how different the learned parameters are for permutation of the data. In this way, we are checking for overfitting. The idea here is that the correct function will learn the shape of the underlying pattern, as opposed to accidental regularities of the dataset.