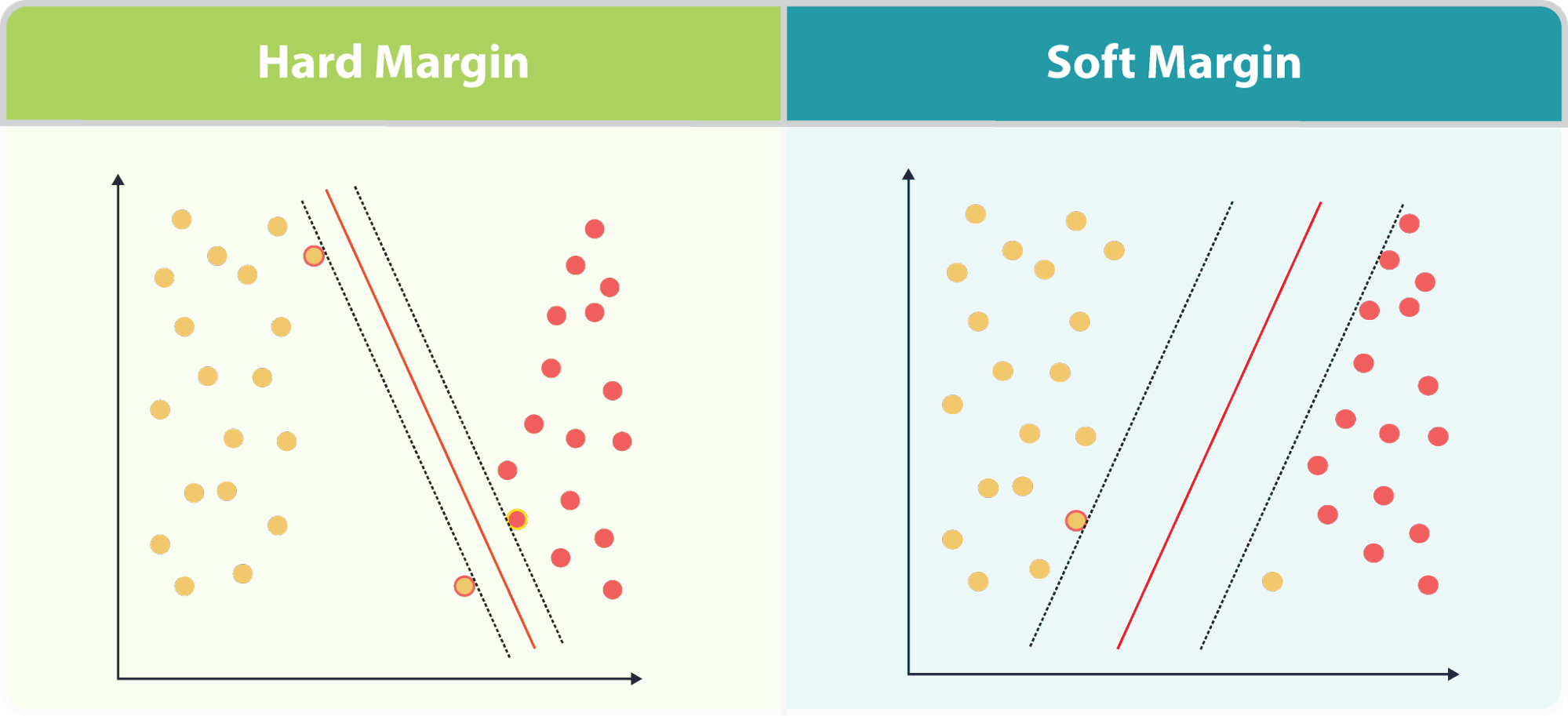
Soft Margin for non-linearly separable data

In almost all real machine learning problems, data are unlikely to be linearly separable due to one of two reasons. One is that the underlying patterns themselves are not linearly separable, the other is that noise has polluted the data, creating a non-linearly separable permutation of the underlying pattern. Classic linear SVM cannot adequately deal with the former problem, but for the latter, we can use the soft margin extension to improve the classic SVM method.

The soft margin formulation of the SVM problem is $$\begin{array}{ll} \underset{\mathbf{w},\xi} {\mbox{minimize}} & \frac{1}{2} \left| \left| \mathbf{w} \right| \right| + C \sum_{i=1}^m \xi_i \\ \mbox{subject to} & \ y_i (\mathbf{w}^T\mathbf{x} + b ) \geq 1 - \xi_i \forall i \\ & \xi_i \geq 0 \end{array}$$

This expression might seem daunting, but it can be understood in extremely simple terms. We are minimizing a joint function, specifically, the sum of two functions. The first is the magnitude of our weights, and the second is the sum of some error terms, $\xi_i$ . Our loss function will drop when we minimize either weight magnitude or error terms.

The slack variable, $C$, defines how heavily we should weigh the error term in our function. If $C$ is large, then we make a much larger difference in the overall function value by minimizing error. If $C$ is small, then the overall function value goes down faster by minimizing weight magnitude. Different $C$ values determine different optimization solutions, and the user must define the value for $C$ whenever an SVM is applied to a task. $C$ is an example of hyper-parameter.

This formulation of the SVM optimization can be solved in the same way as the hard-margin method, with a quadratic program. However, this new formulation can also be rewritten as an unconstrained optimization problem, which can be solved via gradient descent or other sampling techniques. The famous Pegasos algorithm is the most famous gradient descent method for this purpose. The unconstrained formulation is written as follows: $$\underset{\mathbf{w}} {\mbox{arg min} } \frac{1}{2} \left| \left| \mathbf{w} \right| \right| + C \sum_{i=1}^m \mbox{max} \left( 0, 1- y_i (\mathbf{w}^T\mathbf{x} + b ) \right)$$

The soft margin extension is the go to method when using SVMs, and is the default mode for almost all common SVM implementations. It is important to note that if the underlying patterns of a problem are themselves not linearly separable, then the soft-margin extension is simply not going to achieve high end performance. We will need to move to kernel SVM to that end. The following section deals with the dual form of the SVM minimization problem. This lends itself readily to kernel SVM.