Geometric Distribution

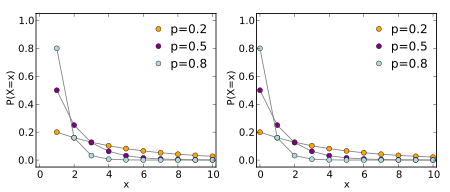
• Notation
  • $T ∼ Geom(p)$

• Interpretation

  • Geometric Distribution studies the number of failures until the first success in independent trials with probability {% math %}p{% endmath %} of success and {% math %}1 - p{% endmath %} of failure on each trial. Geometric Distribution is a special case of the negative binomial distribution and it deals with the number of trials required for a single success.

• Type:
  • Discrete

• Parameter(s):
  • $p$ - probability of success on a single trial

• Probability Density Function:
  • $f(x) = p(1-p)^{x-1}$

• Range:
  • $p[0, 1]$
  • $T(0, \infty)$
  • $x(0, \infty)$

• Mean:
  • $E(T) = \frac{1}{p}$

• Variance:
  • $Var(T) = \frac{1 - p}{p^2}$

• Application:

  • The geometric distribution is the simplest probability distribution about the waiting time distribution.
  • The geometric distribution has the “memoryless” property, that is, it forgets what has happened. The probability of getting an additional {% math %}s-t{% endmath %} failures is the same as the probability of observing {% math %}s-t{% endmath %} failures at the start of the sequence if we already observed {% math %}t{% endmath %} failures. For example, in coin flipping, we can use geometric distribution to estimate the number of tosses needed for getting the first head.