Geometric Interpretation

In its basic form, the perceptron can be functionally visualized as below.

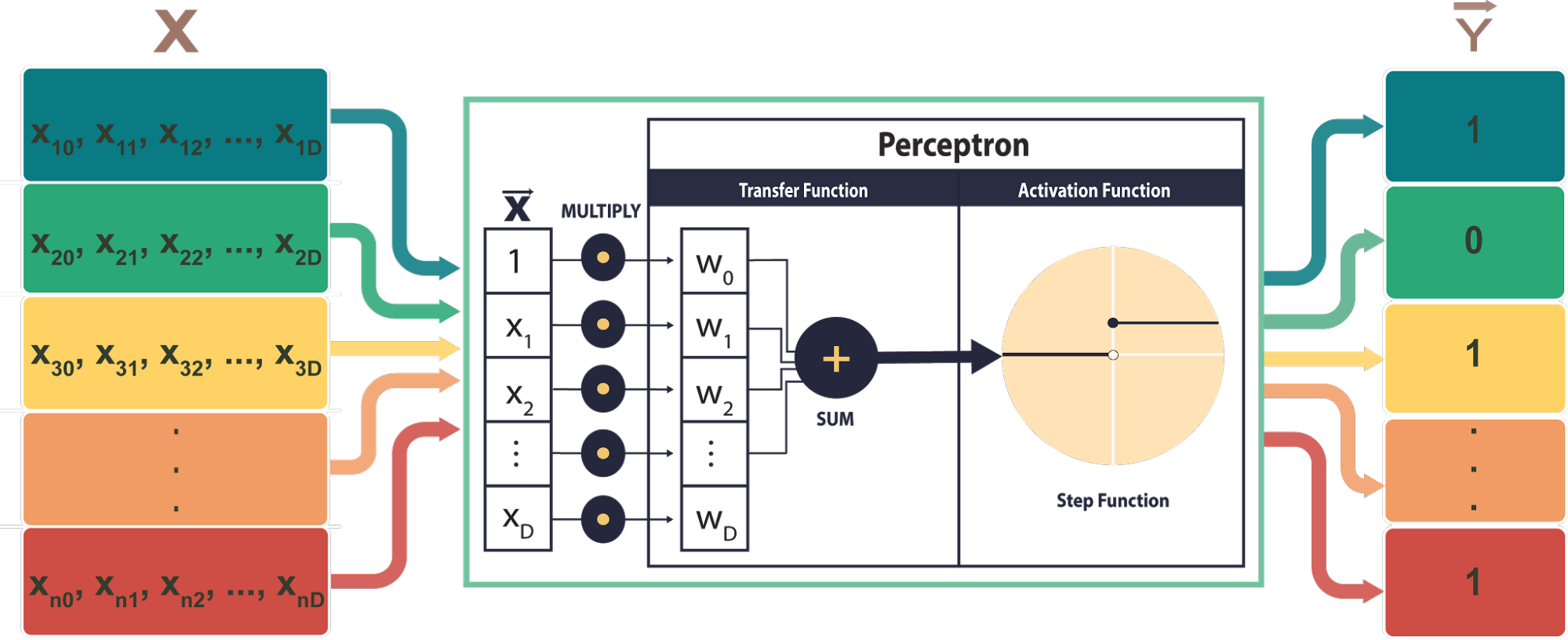
In this case, the vector $X$ is an input vector of dimensionality $n$,$x\subset\Re^n$, whose elements are the values $x1,...xn$. Note that a ‘1’ is concatenated to the front of any input vector. These values are all multiplied by a corresponding weight, $w_0$ to $w_n$. $w_1$ to wn are called correlating weights, and $w_0$, which is multiplied against the ‘1,’ is called the bias.

These products are all summed, generating a weighted sum of the inputs. Note that this weighted sum is equal to the dot product of the $x$ vector and a vector of the weights, $w$, such that

$$w_0+x_1w_1+x_2w_2 + \dots + x_n w_n = \vec{w} \cdot \vec{x}$$

This weighted sum is then put through an activation function, which is a function with an output space of $\{0,1\}$ that has the form:

$$s(\vec{w}\cdot \vec{x}) = \begin{matrix} 1 & if \ \vec{w}\cdot \vec{x}\geq 0\\ 0 & if \ \vec{w}\cdot \vec{x}< 0 \end{matrix}$$

Put simply, this function just checks the sign of its input, and returns 0 if the input is negative, 1 otherwise.

Taken all together, the perceptron classification model is simply $$\hat{y} = s(\vec{w} \cdot \vec{x})$$

where the left side of the equation is the predicted label for a point, $s$ is the activation function described above, and the dot product $w \cdot x$ is equal to the weighted sum of the elements of that point. Notice how this operation corresponds perfectly to the diagram of the perceptron structure shown above.

If the weights are used to define some decision boundary, then the above classification function tells us whether data $x$ is above or below the boundary. This is done mathematically by seeing if $w \cdot x$ is greater than or less than zero.

Let’s consider the decision boundary of the perceptron algorithm that is given by the equation:

$$\vec{w} \cdot \vec{x} = 0$$

This is the place where the model output changes is the place where the linear combination $w \cdot x$ changes sides.

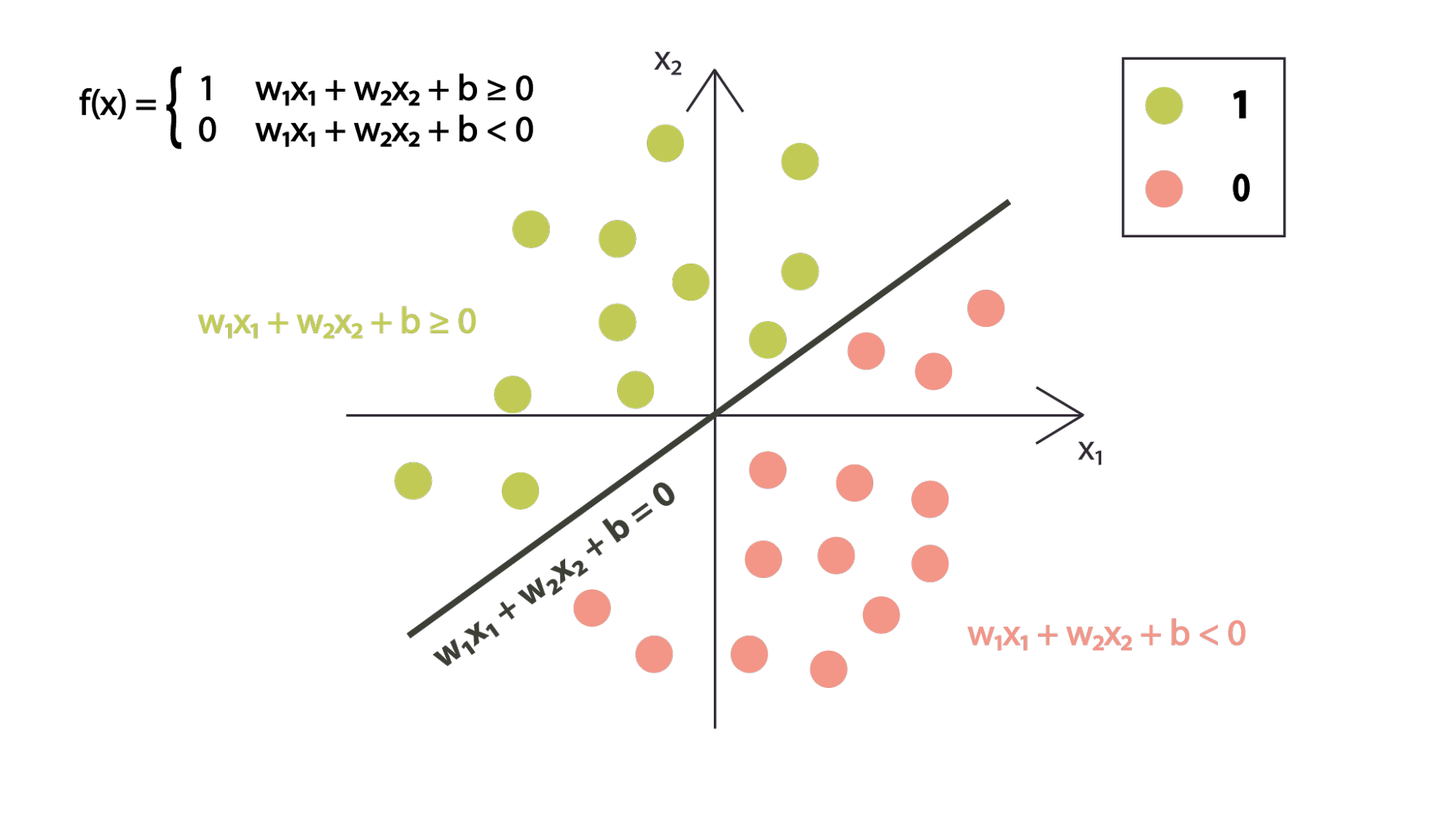
Notice that the region where the dot product of the input and weights is positive, which is where our classifier would return a 1, will fall above the decision boundary, and the region where the product is negative, where any point would be classified as negative, will fall below the decision boundary.

In sum, we have seen how an internal set of weight values can be used to define a decision boundary. We have also seen how any point can be computed as being above or below that boundary, simply by taking the sign of the linear combination of that point and the weights. The perceptron model is a function that does precisely this, and is used to classify points. This is done by finding a decision boundary, or equivalent set of weights, that separates the two classes of data for some training set with the hope that the future data will resemble the sample data in pattern.