Convergence and Limitation

Although the perceptron learning rule is simple, it is quite powerful. In fact, it can be shown that the rule will always successfully find a set of weights that separate the data as shown above, given that such a set exists. The perceptron learning rule is guaranteed to converge to a solution in a finite number of steps, so long as a solution exists. This brings us to an important question. What problems can a perceptron solve?

Recall that a perceptron is able to divide the input space into two regions by a linear boundary. If we have a dataset wherein a line can be drawn that separates the two classes we’re interested in, then the perceptron is an excellent choice for classifying on that set, as it is guaranteed to find a working solution. But in reality, very few datasets afford such a simple solution. The dataset for which a perceptron can work is called a linearly separable dataset, which form a very small minority of real world case problems.

Below is an example of an AND-gate set, which has two classes, white for 0 and black for 1. We can see that for such a set, the perceptron is guaranteed to find a working solution.

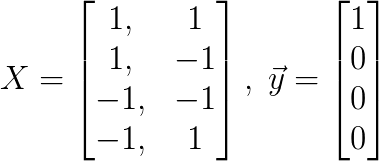
We can see that for such linearly separable dataset, the perceptron is guaranteed to find a working solution.

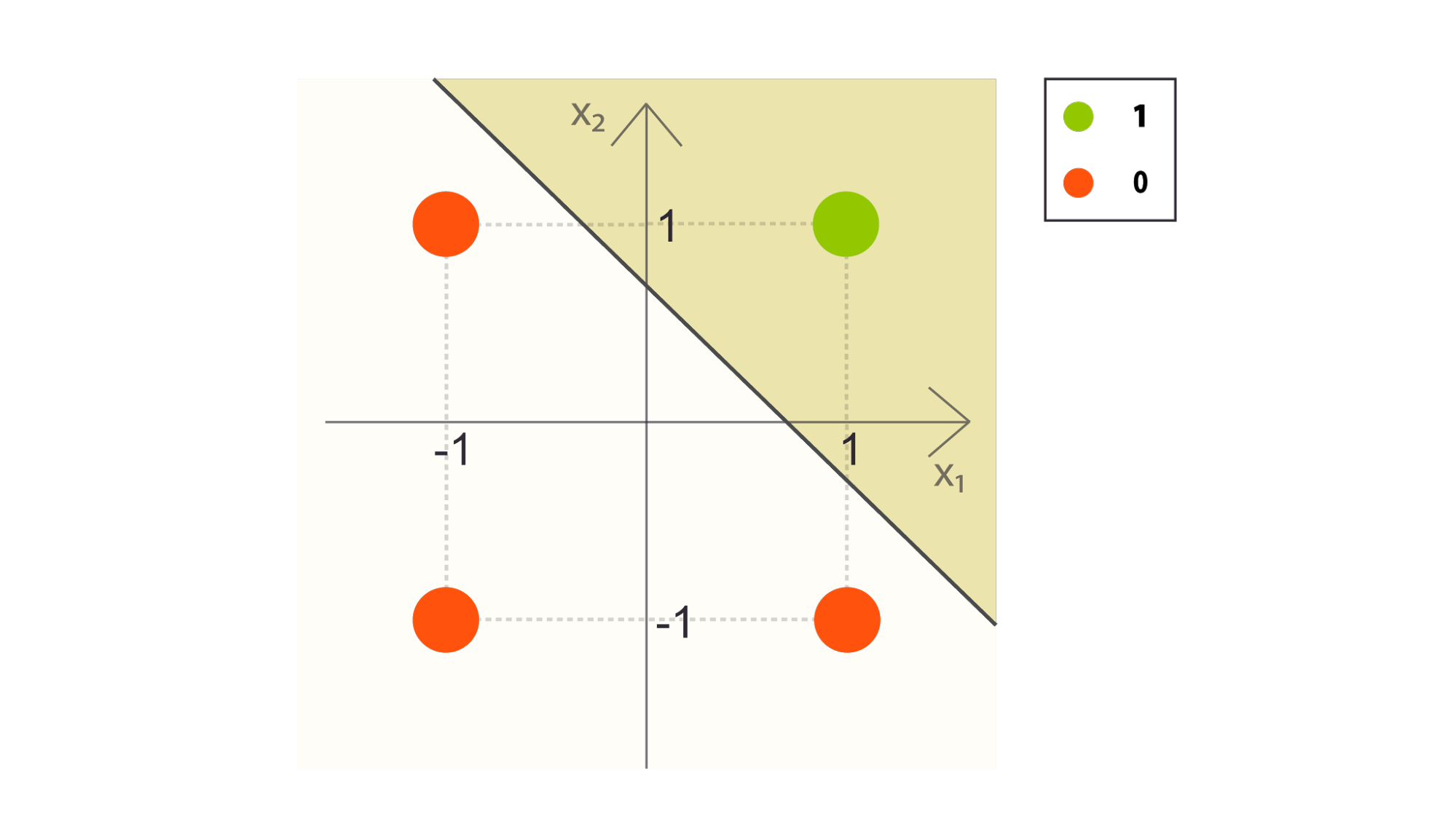
Below is an example of an XOR-gate set, which has the same classes as above. Notice that there is no line that can separate these four points by class.

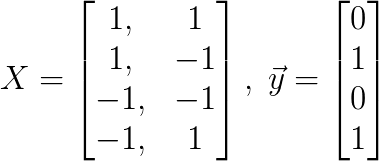
Notice that there is no line that can separate these four points by class, which means we cannot define the every point of class 1 on one side and every point of class 0 on the other.

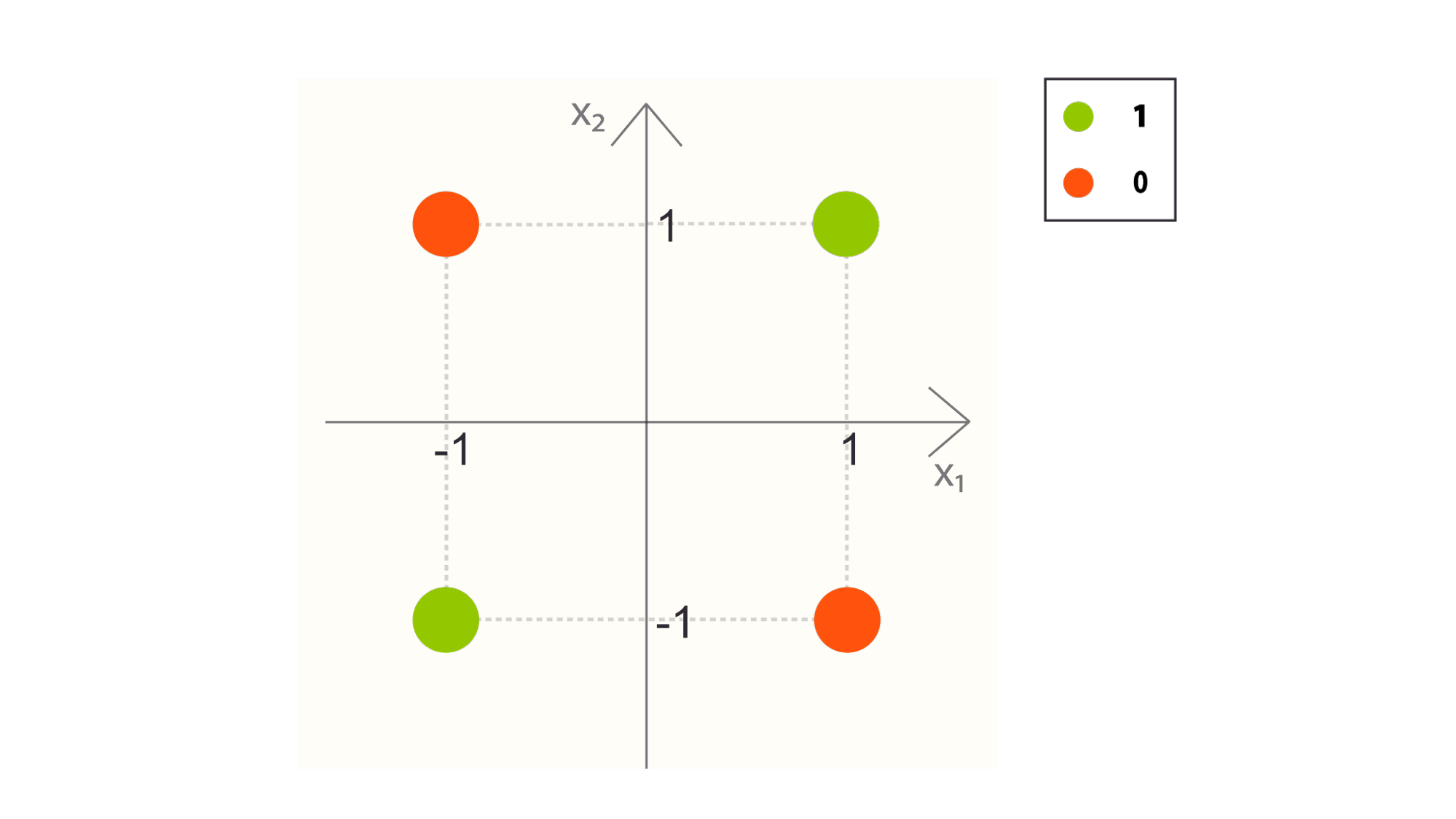
The humble perceptron simply won’t work well on such non-linearly separable dataset. The training algorithm we have defined above will never converge, meaning that it will continue to search until it is stopped. While there are some extensions to the perceptron, including stochastic perceptron learning, there is a hard limit on how well the method can work for real world data. The perceptron is not used except for the simplest tasks, or those that require extremely light computational costs.