## Theory and Knowledge

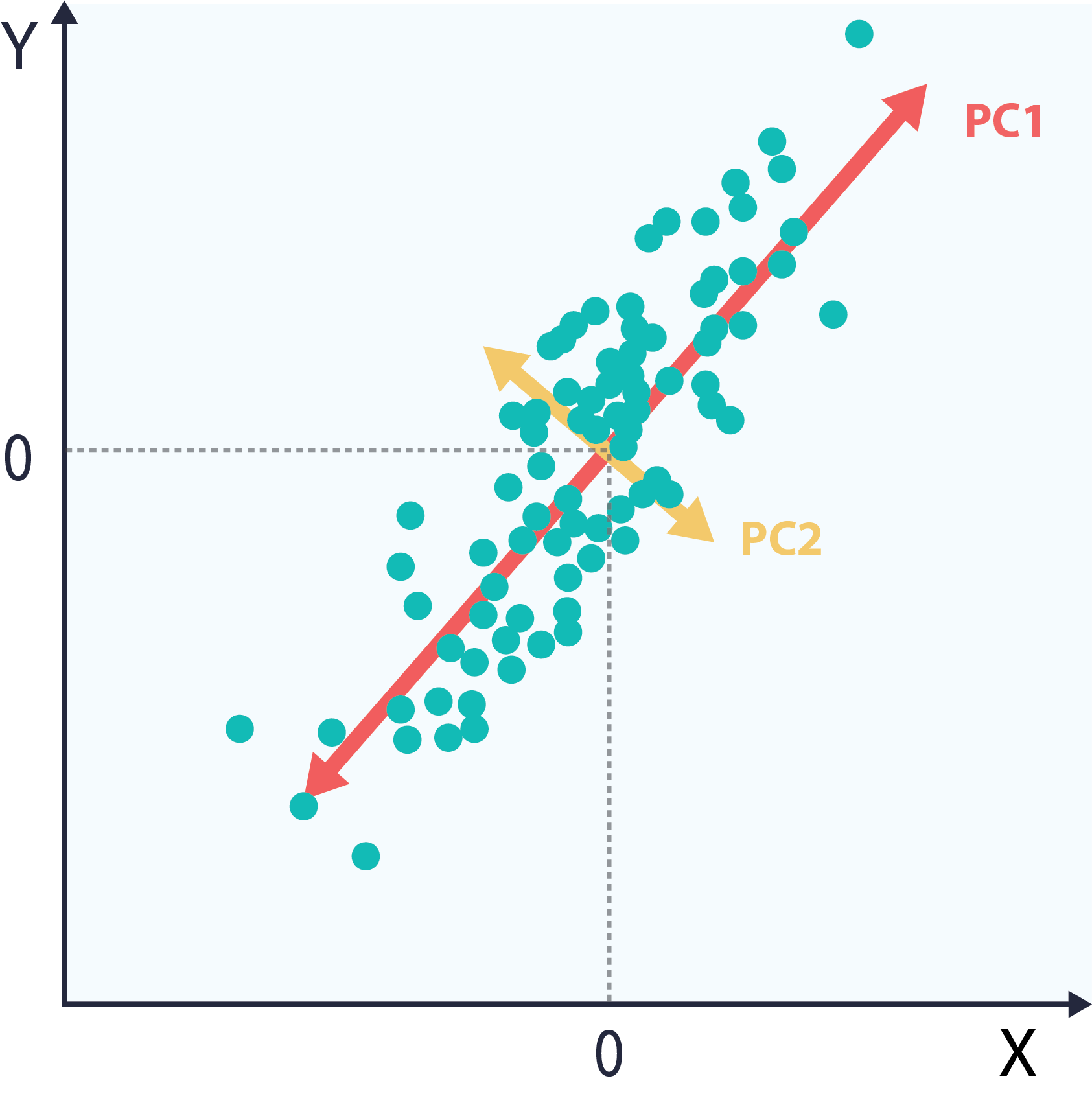
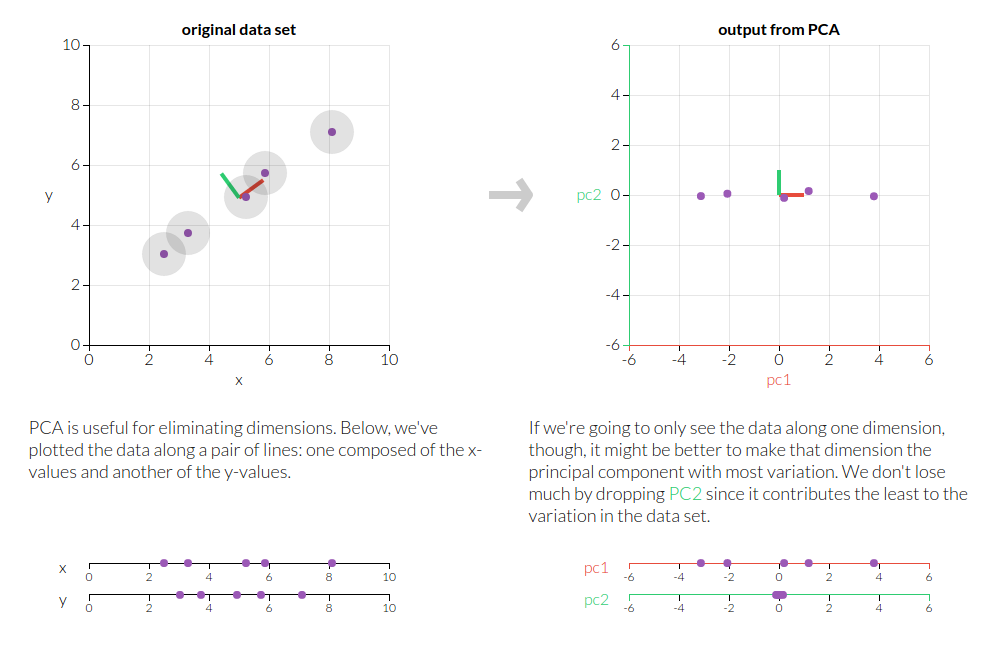
PCA requires a firm grasp of post-calculus linear algebra, specifically eigenvectors and eigenvalues, projections, bases, and vector spaces. It is one of the oldest solutions to the dimensionality reduction problem. The dimensionality reduction problem refers to the ideal way of dropping dimensions for computational simplicity. Consider a simple two-dimensional dataset. The naive method of reducing dimensions is simply to omit some of the dimensions of the corresponding data matrix. Consider the following 2-d image.

The naive solution would fail in this case, as simply omitting either the x or y values would not preserve the structure of the data.

This failing is especially problematic in higher dimensional data. PCA is a more sophisticated solution, and is often the first one taught for this problem. PCA computes the most meaningful directions of the dataset, called the principal components, and uses them as a basis to re-orient the dataset. The principal components are a set of orthogonal vectors that correspond to the directions of greatest to least variance in the data.