Dual Language formulation for kernels

Recall that the dual problem for classic SVM is to maximize the following function $L$ over $\alpha$
$L_D(\vec{\alpha}) = \sum_{i=1}^l \alpha_i - \sum_{i=1}^l \sum_{j=1}^l \alpha_i \alpha_j y_i y_j\vec{x_i}^T\vec{x_j}$

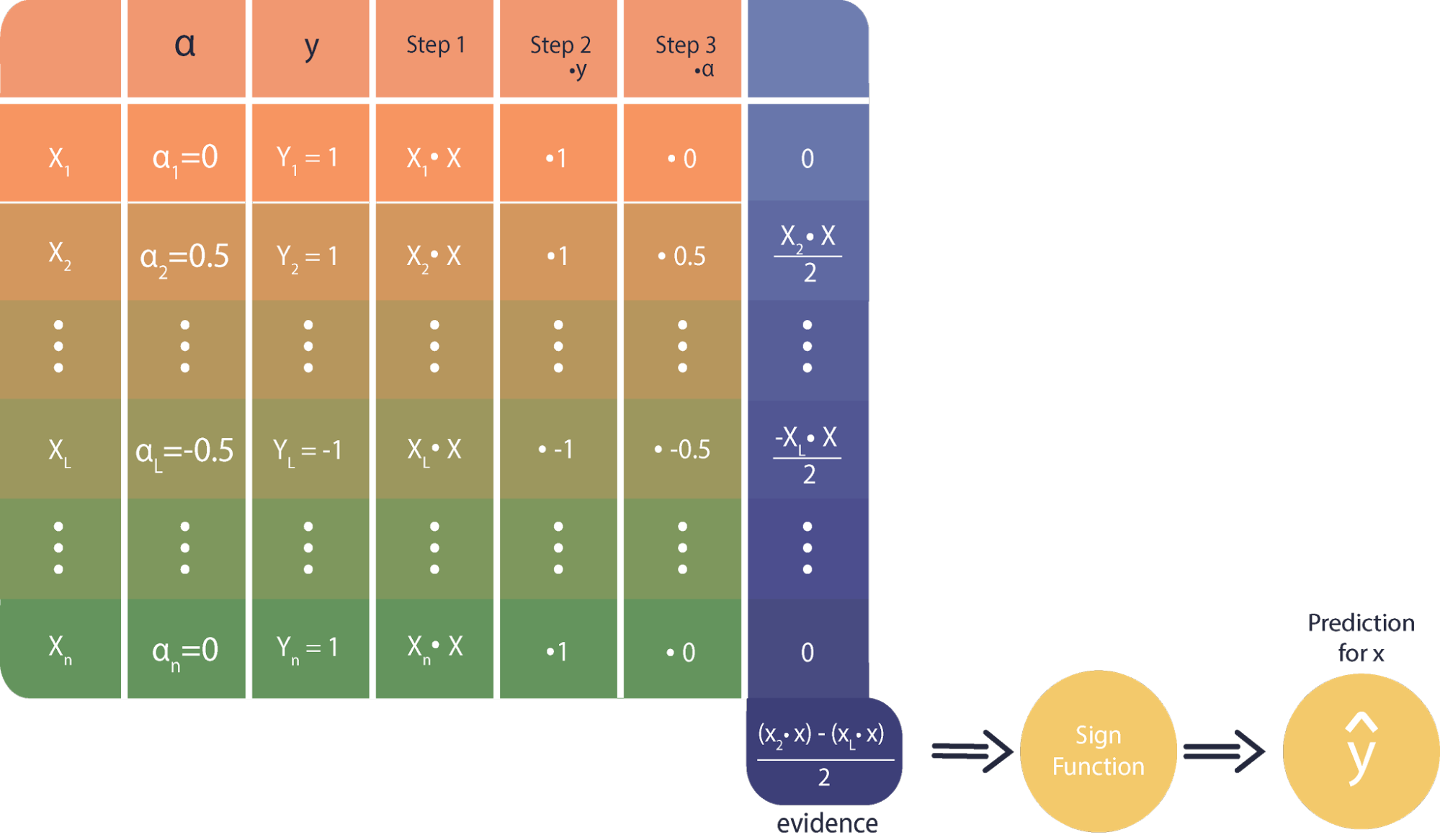
Notice that both the training form, as well as the classification form, are written in terms of dot products between vectors. These dot products need to be understood as similarity functions between these points. The logic of the classifier is that a set of vectors, called the support vectors, are compared against a new point to be classified. The resulting similarity values are combined with the class and importance value of the support vectors. These combined values are summed; the sign of this sum determines the predicted class of the point.

Subject to $(1) \sum_{i=1}^l \alpha_i y_i = 0$, $(2) \alpha_i \gt 0 \ for \ i = 1, \dots, l.$

For kernel SVM, with each $x$ mapped to some higher dimensional vector $\Phi(x)$, the equation becomes
$L_D(\vec{\alpha}) = \sum_{i=1}^l \alpha_i - \sum_{i=1}^l \sum_{j=1}^l \alpha_i \alpha_j y_i y_j\Phi(\vec{x_i})^T\Phi(\vec{x_j})$

with the optimal weights given by

$$\begin{align} \vec{w_o} = \sum_{i=1}^l\alpha_{i,o}y_i\Phi(\vec{x_i}) \end{align}$$

and the optimal plane given by

$$\begin{align} \vec{w_o}^T\vec{x} + b_o = \sum_{i=1}^l\alpha_{i,o}y_i \Phi(\vec{x_i})^T\Phi(\vec{x}) + b_o = 0 \end{align}$$

and the optimal decision function given by

$$\begin{align} g(\vec{x}) = sgn(\vec{w_o}^T + b_o) = sgn(\sum_{i=1}^l \alpha_{i,o}y_i\Phi(\vec{x_i})^T\Phi(\vec{x}) + b_o) \end{align}$$

The explicit coordinates in the higher dimensional mapping space, and even the mapping function $\Phi$ become unnecessary when we define a function $K(x_i , x) = \Phi(x_i)^T\Phi(x)$, the so called kernel function, which directly calculates the value of the dot product of the mapped data points in some feature space. We can avoid explicitly computing $\Phi(x)$ for any point, or handling the dot product of points in $\Phi(x)$ space. The only drawback here is that we have to use some well defined function $K$ that we know corresponds to some useful feature transformation $\Phi(x)$.

Thus, using Kernel function, we can write the equation of dual formulation as
$L_D(\vec{\alpha}) = \sum_{i=1}^l \alpha_i - \sum_{i=1}^l \sum_{j=1}^l \alpha_i \alpha_j y_i y_jK(\vec{x_i},\vec{x_j})$.