What is kernel SVM?

Kernel SVM is an extension to dual form SVM. It uses the so called kernel trick to deal with classification problems of non-linearly separable patterns. The Kernel SVM replaces the inner product operation within the dual SVM formulation, with a Kernel function, where that kernel corresponds to the similarity of two vectors projected into a high dimensional space. Replacing the dot product with a kernel function allows us to perform nonlinear classification without explicitly mapping our data into a high dimensional space, leveraging all the advantages of feature mapping without all the computational costs.

This article will review some key terms, including dot products and projecting data into a higher dimension space. It will introduce the notion of a kernel, explain the theory and usage of the kernel SVM, and describe some commonly used kernels as well as their uses.

The similarity function

A similarity function $K(\vec{v}, \vec{w})$ is any function over two D-dimensional vectors that returns a scalar value, where the scalar output for some pair of vectors is proportional to some measure of ‘similarity’ between the two vectors. Formally, let’s just define a similarity function as a function that maps two vectors of D-dimensions to a scalar.

$$\begin{align} K: \mathbb{R}^{D \times 2} \rightarrow \mathbb{R} \end{align}$$

Note that one of the simplest possible similarity functions is the dot product,

$$K(\vec{v},\vec{w}) = \vec{v}\cdot\vec{w} = \sum_{i=1}^{D}v_{i}w_{i}$$

The reason that the dot product can be used as a similarity function is because it takes two vectors as input, and is inversely proportional to the cosine of the angle between the two inputs, $u \cdot v=|u||v|cos \theta$ Meaning that the dot product is equal to the product of the two vector’s lengths, when those vectors point in the same direction. The dot product is $0$ when the two vectors are orthogonal. The dot product is the negative product of the two vectors’ lengths when they point in opposite directions. We can think of the dot product of two vectors as the product of their magnitudes, scaled by how parallel they are.

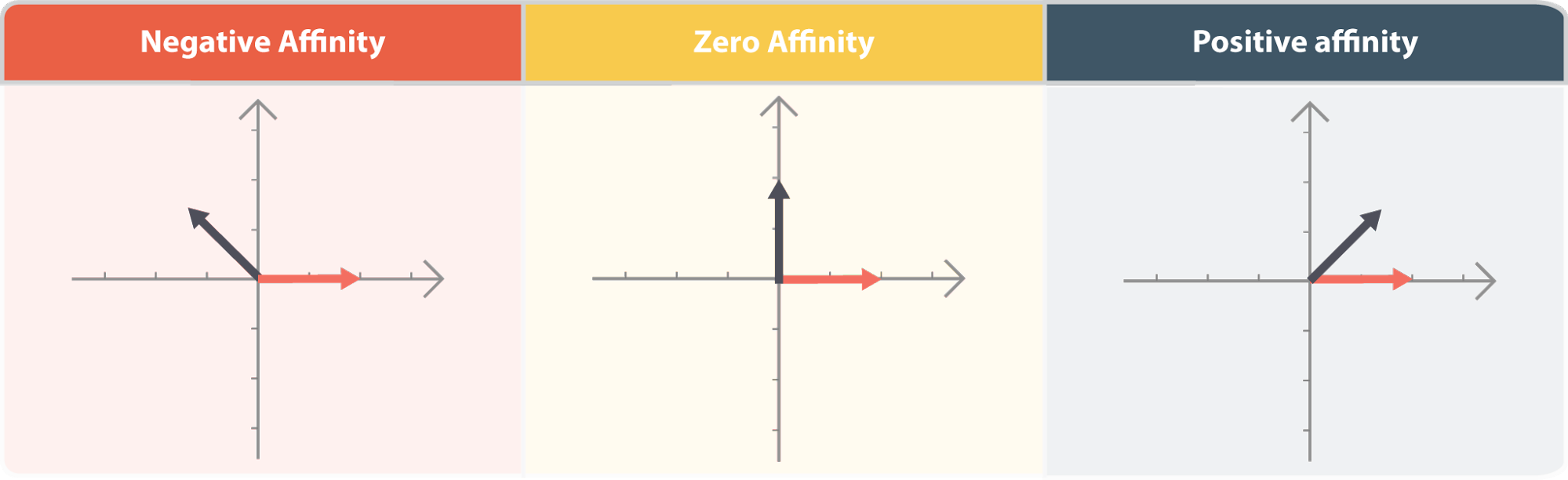
We can use this to find a normalized similarity measure, called the affinity, between two vectors, which we define as the following:

$\frac{u \cdot v}{||u|| \cdot ||v||} = cos\theta$

This gives us a number between $-1$ and $1$ that tells us how parallel two vectors are.