What is depth-limited search?
The depth-limited search (DLS) method is almost equal to depth-first search (DFS), but DLS can work on the infinite state space problem because it bounds the depth of the search tree with a predetermined limit L. Nodes at this depth limit are treated as if they had no successors.
Now use the example in DFS to see what will happen if we use DLS with .
Below is the graph we will traverse. Same as DFS, we use the stack data structure S1 to record the node we’ve explored. Suppose the source node is node a.
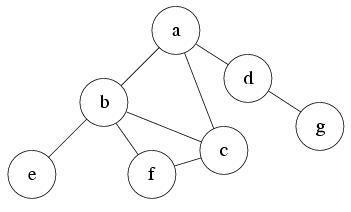
S1:
At first, the only reachable node is a. So push it into S1 and mark as visited. Current level is 0.
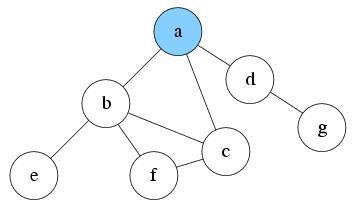
S1: a
After exploring a, now there are three nodes reachable: node b, c and d. Suppose we pick node b to explore first. Push b into S1 and mark it as visited. Current level is 1.
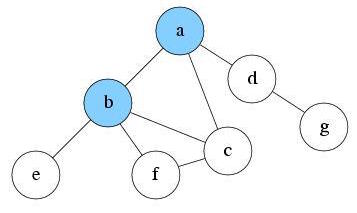
S1: b, a
Since current level is already the max depth L. Node b will be treated as having no successor. So there is nothing reachable. Pop b from S1. Current level is 0.

S1: a
Explore a again. There are two unvisited nodes c and d that are reachable. Suppose we pick node c to explore first. Push c into S1 and mark it as visited. Current level is 1.
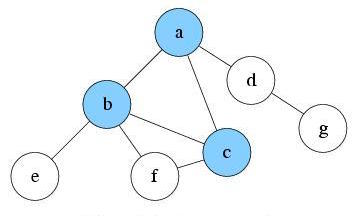
S1: c, a
Since current level is already the max depth L. Node c will be treated as having no successor. So there is nothing reachable. Pop c from S1. Current level is 0.

S1: a
Explore a again. There is only one unvisited node d reachable. Push d into S1 and mark it as visited. Current level is 1.
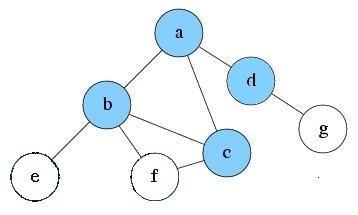
S1: d, a
Explore d and find no new node is reachable. Pop d from S1. Current level is 0.

S1: a
Explore a again. No new reachable node. Pop a from S1

S1:
S1 is empty now. DLS will be finished.