What is depth-first search?
Formally, depth-first search (DFS) is an algorithm for traversing tree or graph data structures. It starts at the root and explores as far as possible along each branch before going back to the upper level.
Now let’s see how DFS works. Below is the graph we will traverse. Unlike BFS, DFS uses a stack data structure, which we will call S. to record the nodes we’ve explored. Stacks are first in, last out. Meaning that if you join the stack, everyone who gets in after you will leave before you. Think of a stack as a bunch of cars sharing a really long parking space. If two cars are parked behind you, they need to move before you can get out.
The DFS algorithm works on the following steps. We add nodes to the stack one at a time, and as soon as a node is put into the stack, it is explored. If it is not connected to any new node, it is immediately removed from the stack. When it is removed, the resulting first node is then re-explored for a new node. If it does connect to new nodes, we add one to the stack, and repeat the process. When the stack is empty, the algorithm has traversed the whole graph, and finished. Obviously, if a goal node is found, then the algorithm ends early.
Suppose the source node is node a.
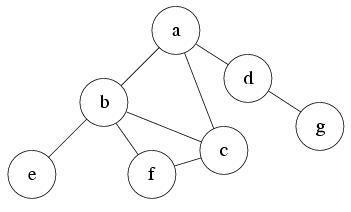
S:
At first, there is only the node a reachable. So push it into S and mark is as visited.
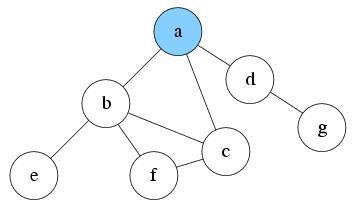
S: a
After exploring a, now there are three nodes reachable: node b, c and d. Suppose we pick node b, randomly. Push b into S and mark it as visited.
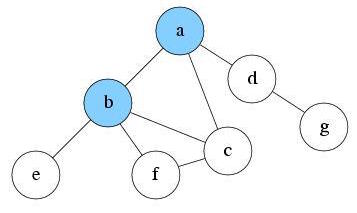
S: b, a
After exploring b, there are three nodes reachable now: node e, f and c. Suppose we pick node c randomly. Push c into S and mark it as visited.
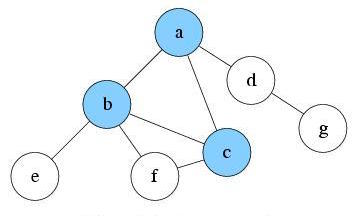
S: c, b, a
Explore c. There is only one unvisited reachable node, f. Push f into S and mark it as visited.
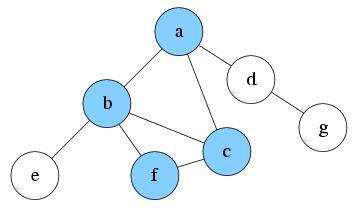
S: f, c, b, a
Explore f and find no new reachable node. Pop f from S.

S: c, b, a
Explore c and find no new node reachable. Pop c from S.

S: b, a
Explore b. A new node e is reachable. Push e into S and mark as visited.
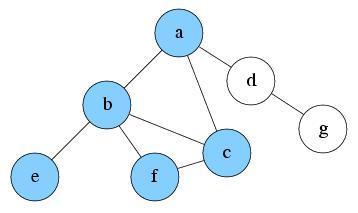
S: e, b, a
As previously, exploring node e will yield no new reachable node. The same is true for b, which we explored next. Pop them from S.

S: a
Explore a. A new node d is reachable now. Push it into S and mark as visited.
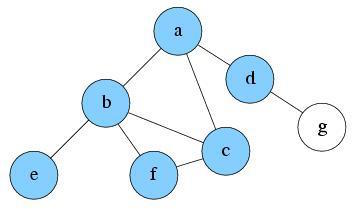
S: d, a
Explore d. Node g is reachable now. Push it into S and mark as visited.
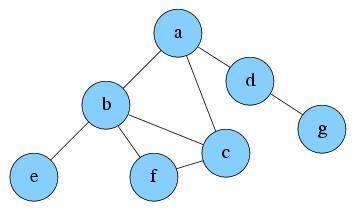
S: g, d, a
Repeating the process yields exploring nodes g, d and a in sequence, which will not introduce any new nodes. Pop them from S.

S:
S is empty now. DFS will be finished and every node reachable from the source a is visited.