Weights and Prediction

The logistic regression works almost identically to the perceptron, except that it returns a stochastic prediction. Like the perceptron, it takes a point as an input, computes the transfer function value on that point, and sends that value to some activation. The main difference is that within a perceptron, the sign function is used to output class labels directly.

Within logistic regression, we replace the sign function with the sigmoid.

$\sigma(z)=\frac{1}{1+e^{-z}}$

This produces a continuous valued approximation of the class labels. As stated above, this can be interpreted as the probability that the correct class for the input point is ‘1’ and the wrong class for the input point is ‘0.’ It’s also the case that the sigmoid output is always closer to either 0 or 1. This allows for direct classification; if you round the sigmoid output to the nearest integer, you get the sign function output.

One should think of the argument to the sigmoid function as a sort of signed “evidence” for one class. Specifically, if the input to the sigmoid is very far from zero, then the value of the sigmoid will be very close to 1 or 0, depending on the sign. If the input is positive, the output will be closer to 1 than 0, and if the input is negative, then the output will be closer to 0 than 1. These two facts are key.

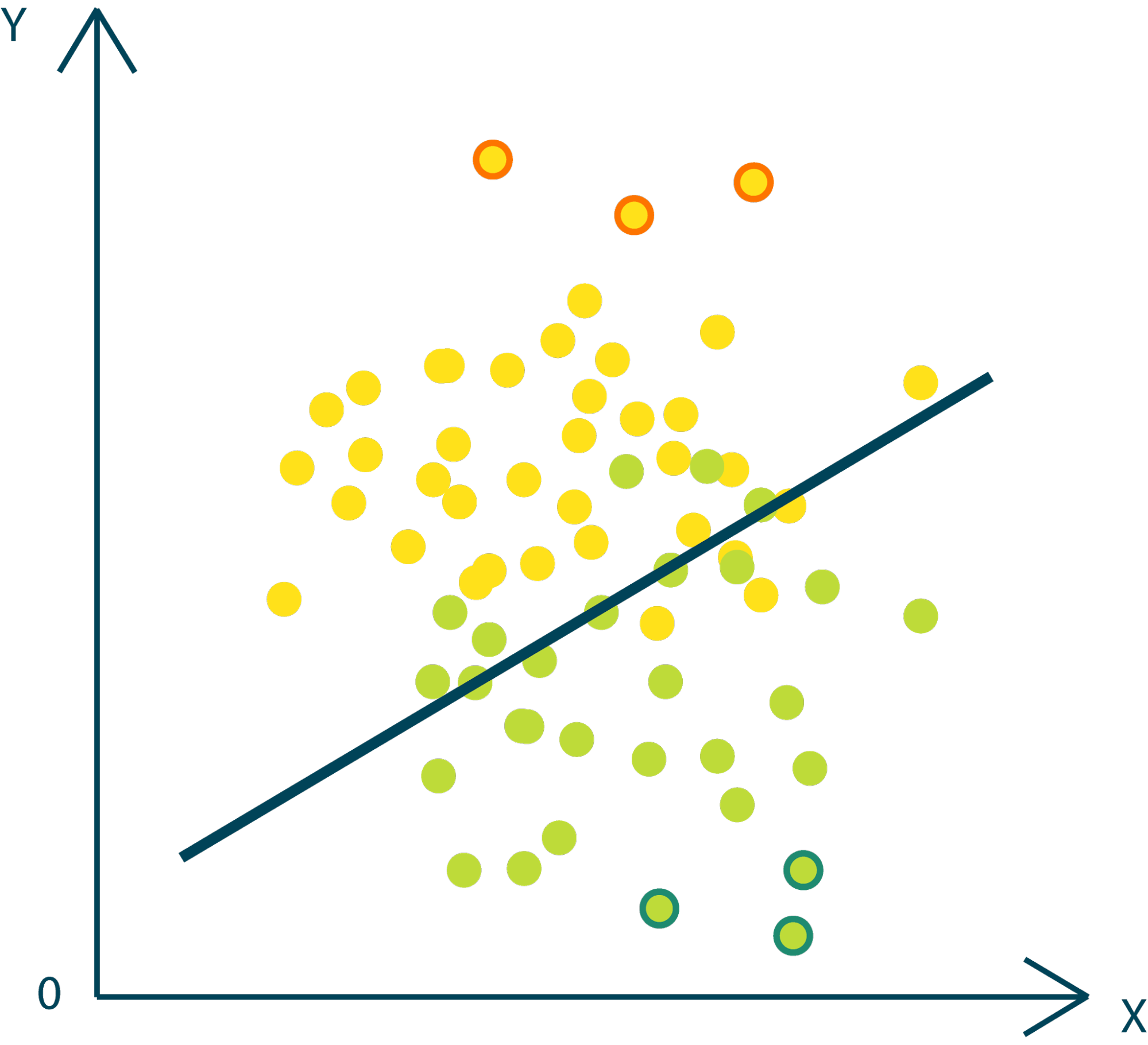
The sigmoid can be used to predict classes for any datapoint. From the two facts we see that the magnitude and sign of the sigmoid argument determine the predicted confidence, and predicted class of our model, respectively. When a logistic regression model returns a value greater than .5, then we say it has predicted class 1, and when the model returns a value less than .5, we say that it has predicted class 0. The predicted class is the nearest integer to the sigmoid output. The closer the output to either integer, then the more confident the model is.

The signed “evidence” value fed into the sigmoid is the transfer function value given the method’s internal weights. Please refer to our article on parametric models and decision boundaries more a deeper consideration of the facts in this section.

We can write the logistic regression model function as $P(C=1|x)=(w_0+w_1x_1+w_2x_2+w_3x_3+\dots +w_dx_d)=(w\cdotx), where w = w_0,w_1,\dots,w_d and x=[1,x_1,x_2,\dots,x_d]$

Note again that this function differs only in the use of the sigmoid in place of the sign function.