Cost Function

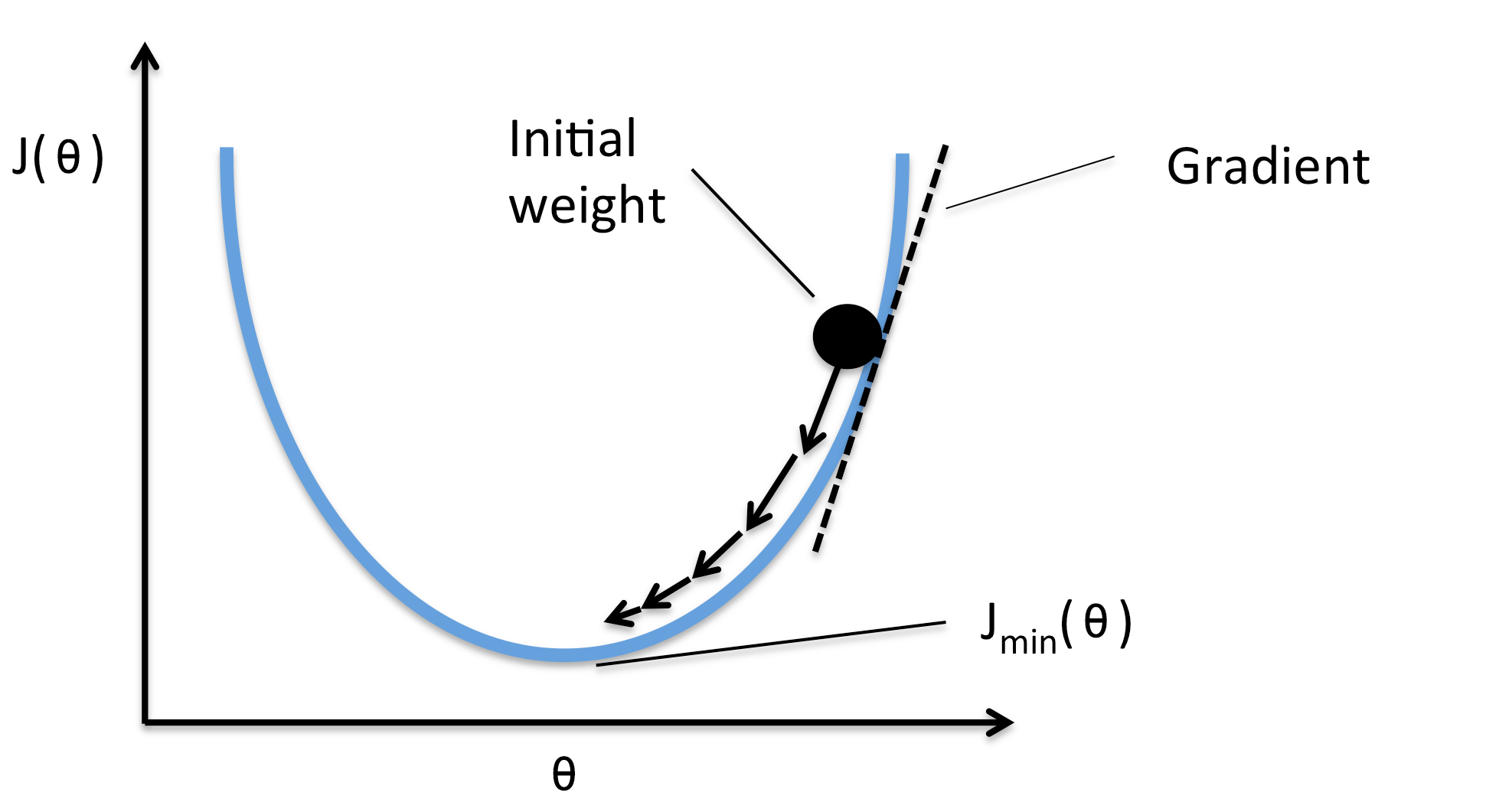
As in all supervised parametric models, training a logistic regression instance on a dataset is the process of finding the ideal weights w that minimize the error between the predictions for that dataset and the true labels. We accomplish this by minimizing a loss function.

If our function returns that the probability of class 1 is .9, then it is fairly certain that the class is 1. If our function returns that the probability of class 1 is .1, then, because the probabilities of the two must add up to 1, we can say that the classifier is .9 sure that the class is 0.

It should be noted that for logistic regression, we are treating the stochastic prediction of the model as the prediction. We are not rounding the sigmoid value to class labels before feeding those values into the loss function. In this way, we are keeping confidence information, and the loss function is minimized when every point in the training set is correctly classified, with high confidence.

For a set of training examples $\{x^{(i)},y^{(i)},{\ for}~i=1,\cdots,n\}$, with binary labels, the following cost function measures how well a given function h classifies the set. Please note that the function his the same function just described, namely, $P(C=1|x)$. Note as well that the summation is across the index of every datapoint and target pair in our set, and so we’re summing across the entire set.

$$\begin{eqnarray*} L(w) = -\sum_{i=1}^{n} y_{i}log(\sigma (w \cdot x_{i})) + (1-y_{i})log(1- \sigma (w \cdot x_{i})) \end{eqnarray*}$$

This is known as the cross entropy function, and it is one of many viable functions to use as a cost. Notice that, like any loss function should, this function is zero when the predicted class of every point, $x^{(i)}$ is equal to the true labels for each point, $y^{(i)}$. To train our classifier, which is the same as finding the weights that minimize this function, it is common to use gradient descent. Gradient descent can be thought of as a more sophisticated version of guess-and-check, where after each check, we use some mathematical properties to change the weights in an informed way. The idea being to incremental move to better and better weights until our classifier has the accuracy we want.