General Rules in Probability

1.Complement Rule

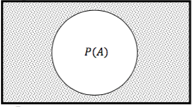
The probability of the complement of A is $P(\bar{A}) = 1 - P(A)$

2. Conditional probability rule

The conditional probability of some event $A$ given some event $B$ is written $P(A|B)$ and refers to the ratio between the area of the intersection and the area of event $B$. $P(A|B) = \frac{P(A \cap B)}{P(B)}$

3. Union rule

The probability of a union of events can be expressed in terms of the probabilities of the events and their intersection $$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$

4. Product rule

Corresponding to the conditional probability rule, the probability of an intersection, also called a joint probability, can be expressed as $$P(A \cap B) = P(A|B)P(B) = P(B|A)P(A)$$

5. Sum Rule

The probability of any event A is equal to the sum of the joint probabilities of that event and any two complementary events. $$P(B) = P(B \cap A) + P(B \cap \bar{A})$$

6. Subset Rules

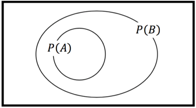
We say that A is a subset of B, written as $𝐴 ⊆ 𝐵$, when the occurrence of event A indicates the occurrence of event B. Properties:

1. P(A \cup B) = P(B)
2. P(A \cap B) = P(A)
3. P(A) \leq P(B)
4. P(B \cap \bar{A}) = P(B) - P(A)
5. P(A|B) = \frac{P(A)}{P(B)}
6. P(B|A) = 1

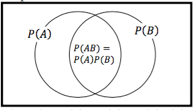
7. Independence Rule

Two events A and B are independent if the probability of B does not depend on A. If A and B are independent, then;

1. $P(𝐴 \cap 𝐵) = P(𝐴)P(𝐵)$
2. $P(A|B) = P(A)$

8. Mutually Exclusive Rule (Disjoint)

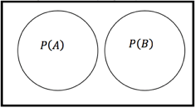
A and B are two mutually exclusive events. The occurrence of event B indicates that the occurrence of A is impossible.

1. $𝑃(𝐴 \cup 𝐵) = 𝑃(𝐴) + 𝑃(𝐵)$
2. $𝑃(𝐴 \cap 𝐵) = 0$

9. Inclusion-Exclusion Rule

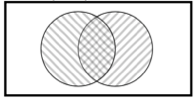
In general, 𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵) − 𝑃(𝐴𝐵) From the venn diagram in the left, we can see that summing of P(A) and P(B) will count P(A ∩ B) twice and thus we need to subtract one P(A ∩ B) from their sum. Note: Mutually exclusive events is a special case for inclusion-exclusion rule. Since for mutually exclusive events $P(A \cap B) = 0, P(A \cup B) = P(A) + P(B)$

10. De Morgan’s Law

De Morgan’s Law describes the effect of complement on the relationship between two events with sets operation.

• Properties:
  • The complement of the union of two sets is the same as the intersection of their complements.
  • The complement of the intersection of two sets is the same as the union of their complements.

11.General rules for 3 or more events

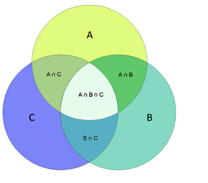
• a) Inclusion-Exclusion Rule

$P(A∪B∪C) = P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)$

• b) Partitions $P(A∪B∪C) = P(ABC)+P(AB\bar{C})+P(\bar{A}BC)+P(A\bar{B}C)+P(AB\bar{C})+P(\bar{A}\bar{B}C)+P(\bar{A}B\bar{C})+P(A\bar{B}\bar{C})$

• c) Complement $P(A∪B∪C) = 1-P(\bar{A}\bar{B}\bar{C})$

• d) Independence Three events A, B and C are independent if they are both mutually independent and pairwise independence. The following set of statements are sufficient to prove event A, B and C are mutually independent.

  • $P(AB) = P(A)P(B)$
  • $P(AC) = P(A)P(C)$
  • $P(BC) = P(B)P(C)$
  • $P(ABC) = P(A)P(B)P(C)$