Characteristics of Bayes net

Explaining away

In the above example, notice that the two causes "compete" to "explain" the observed data. Hence $$S$$ and $$R$$ become conditionally dependent given that their common child, $$W$$, is observed, even though they are marginally independent. For example, suppose the grass is wet, but that we also know that it is raining. Then the posterior probability that the sprinkler is on goes down:

$$P(S=1|W=1,R=1) = 0.1945$$

This is called "explaining away". In statistics, this is known as Berkson's paradox, or "selection bias". For a dramatic example of this effect, consider a college which admits students who are either brainy or sporty (or both!). Let $$C$$ denote the event that someone is admitted to college, which is made true if they are either brainy ($$B$$) or sporty ($$S$$). Suppose in the general population, $$B$$ and $$S$$ are independent. We can model our conditional independence assumptions using a graph which is a $$V$$ structure, with arrows pointing down:

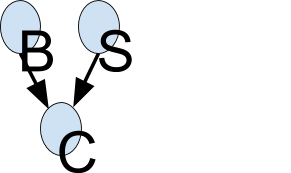
Now look at a population of college students (those for which C is observed to be true). It will be found that being brainy makes you less likely to be sporty and vice versa, because either property alone is sufficient to explain the evidence on $$C$$ (i.e., $$P(S=1 | C=1, B=1) \leftarrow P(S=1 | C=1)$$). (If you don't believe me, try this little BNT demo!)

Top-down and bottom-up reasoning

In the water sprinkler example, we had evidence of an effect (wet grass), and inferred the most likely cause. This is called diagnostic, or "bottom up", reasoning, since it goes from effects to causes; it is a common task in expert systems. Bayes nets can also be used for causal, or "top down", reasoning. For example, we can compute the probability that the grass will be wet given that it is cloudy. Hence Bayes nets are often called "generative" models, because they specify how causes generate effects.

Causality

One of the most exciting things about Bayes nets is that they can be used to put discussions about causality on a solid mathematical basis. One very interesting question is: can we distinguish causation from mere correlation? The answer is "sometimes", but you need to measure the relationships between at least three variables; the intuition is that one of the variables acts as a "virtual control" for the relationship between the other two, so we don't always need to do experiments to infer causality.